Catobyte

A simple introduction to machine learning

Published on 16th of March 2025

1. What is Machine Learning?

Machine learning is a computer science field that allows computers to learn and adapt based on data, without requiring explicit programming for each specific task. As Oxford Languages defines it, machine learning is “the use and development of computer systems that are able to learn and adapt without following explicit instructions, by using algorithms and statistical models to analyze and draw inferences from patterns in data.”

One type of machine learning is a neural network. But before diving into neural networks, let’s take a look at a simpler example of machine learning to build a solid foundation: predicting house prices.

A Real-World Example: Predicting House Prices

Suppose you want to predict the price of a house based on some characteristics, like the number of bedrooms, the house’s size, location, and the year it was built.

First, you’d gather a dataset of houses whose prices you already know. This data can be represented in a table, where each row is a record of a house with columns for different characteristics (known as features or predictors) like size, bedrooms, location, and year built. The column containing the price is our target or dependent variable—it’s the value we’re trying to predict.

Size (sq mt)	Bedrooms	Location (Zip)	Year Built	Price (Simoleons)
1500	3	94121	2005	§700,000
2500	4	94122	2010	§1,000,000
1200	2	94123	1998	§500,000

We’ll use this data to train our model.

Linear Regression: A Simple Model for Prediction

To make this prediction, we can start with a simple model called linear regression. In essence, linear regression looks for a straight-line relationship between the features and the target.

Imagine that each row of data is a point in a dimensional space. For example, if we only used the feature size, we could plot the data points in a 2D space, where the x-axis represents size and the y-axis represents price.

In this scenario, linear regression would fit a line to the data that best explains the relationship between house size and price.

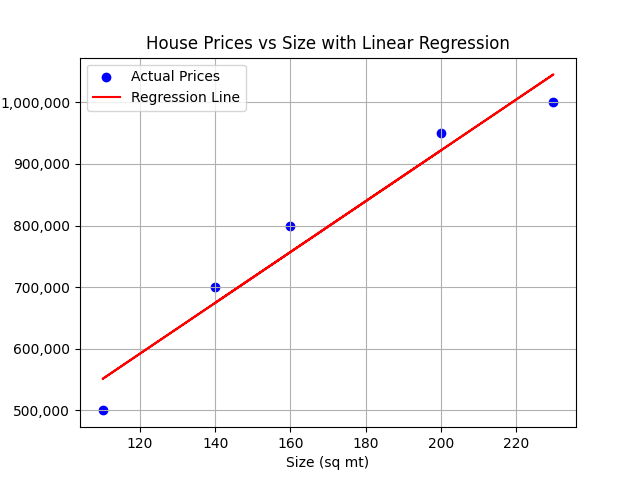
In this scenario linear regression would fit a line to the data that best explains the relationship between house features and price.

Now, let’s add complexity. Imagine using two features instead of one—say, size and the number of bedrooms. Now, our data points would be distributed in a 3D space: the x-axis could represent size, the y-axis could represent bedrooms, and the z-axis would be the price of the house. Here, instead of a line, the regression would fit a plane to the data.

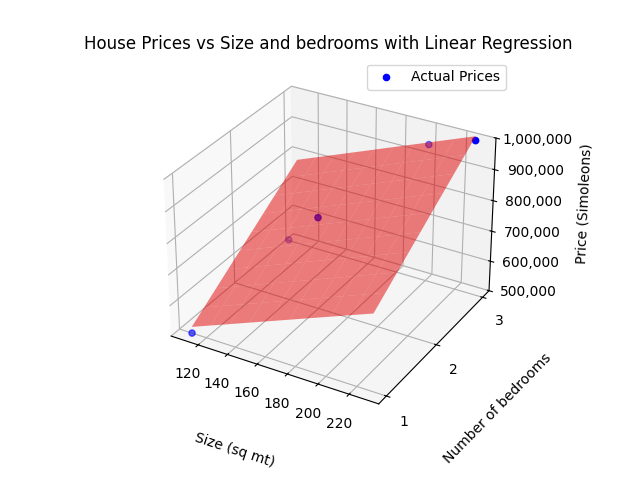
As we add even more features, it’s hard to visualize. For an example with n features, each record would become a point in an (n+1)-dimensional space. In this case, our regression model fits an hyperplane (the term used when we move beyond three dimensions) that best represents the data points.

Once this hyperplane is built, we can use it to predict unknown values. When we create this hyperplane, we are training the model. To evaluate our model, we could keep part of the data for testing, input new feature values, and see how close the predicted price is to the actual price.

Finding the Best-Fit Line, Plane, or Hyperplane: The Formula

In linear regression, the formula for the model is:

Price = β₀ + β₁ * Feature_1 + β₂ * Feature_2 + ... + βₙ * Feature_n

Each feature has a coefficient , which reflects how much impact it has on the target. β₀ is the intercept, or base price, when all features are zero.

In our house price example, this could look like:

Price = β₀ + β₁(Size) + β₂(Bedrooms) + β₃*(Location) + β₄*(Year built)

Our goal is to find values for these coefficients that best fit the data. There are different ways to calculate these values; we’ll look briefly at two of them: Least Squares and Gradient Descent.

Method 1: Least Squares

The Least Squares method gives us an exact solution by solving mathematical equations based on the data. In cases with a single feature, it’s quite efficient, as you only need to go through each data point once. But when you have multiple features, it requires more complex calculations (matrix operations), which may become impractical for large datasets.

Method 2: Gradient Descent

Gradient Descent is an iterative method and is often preferred when dealing with multiple features or large datasets. Here’s a simplified version of the steps:

1. Start with a Guess: Begin with a random line that doesn’t fit the data well. This line has a slope and intercept (position).

2. Check How Far Off You Are: For each house in the dataset, measure how far the predicted price is from the actual price.

3. Adjust the Line: Adjust the line slightly based on how far off you were. If the line’s predictions were too high, adjust it downward; if too low, adjust it upward. Similarly, tweak the slope if it’s too steep or too flat.

4. Repeat: Continue adjusting the line little by little. Each adjustment makes the line fit the data more accurately.

5. Stop When It’s Close Enough: When the line fits the data well enough, we stop adjusting.

Why does this work? Think of it like aiming a dart at a target. Each throw (or adjustment) helps you get closer, and over time, you “learn” to hit near the bullseye.

So there you have it—a real-world example of using machine learning and linear regression to predict values based on data. There are many more methods for making predictions with machine learning. I recommend visiting the scikit-learn website to deepen your understanding of these methods. With this foundation, you now have a basic idea of how machine learning works, and you’re ready to begin exploring this fascinating field in more depth.